The BGGS sea gravimeter system KSS32-M is working as a standlalone device. Once configured, the user-defined data interface (serial RS232, Ethernet) provides the gravity measurements right after the system has powered-up.
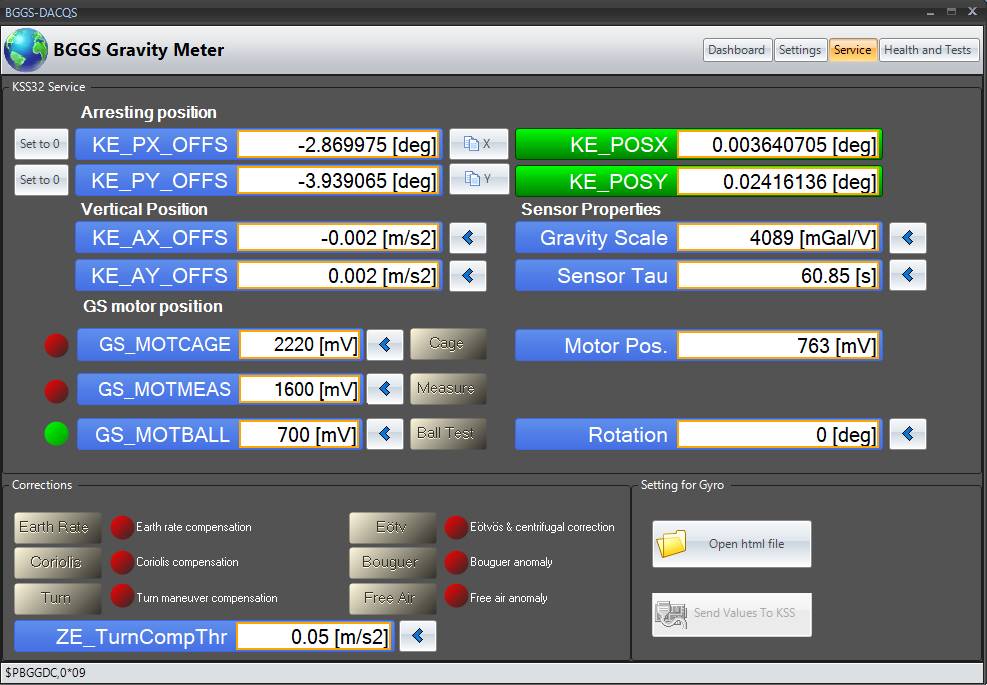
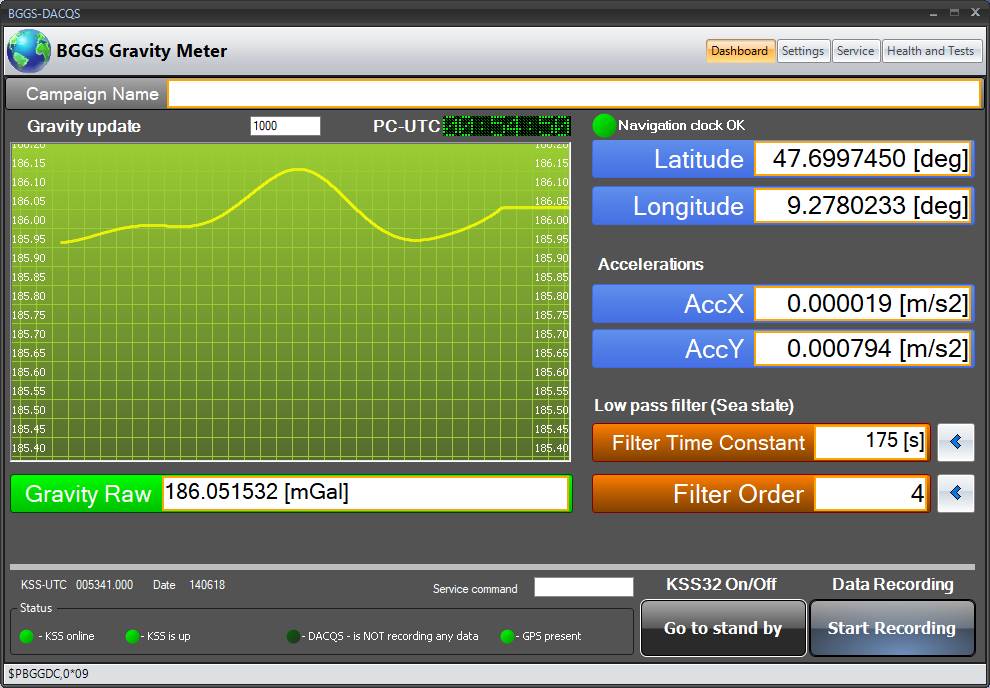
To control, parameterize and monitor the system, as well as to display the gravity measurements, the DACQS software can be used. DACQS can be executed on standard Windows-operated computers/laptops (usually part of the delivery scope).
Software-based compensations and corrections
With its Gravitymeter System KSS32M, BGGS offers a state-of-the-art, gyro-stabilzed platform combined with the proven, updated BGGS sensor GSS32 (spring and mass system with magnetic compensation). Compared to the predecessor KSS31M, the new platform integrates all electronics (ZE), power supply (PS) and interfaces which results in a very compact sea gravimeter. All user interaction, data visualization and more is done via the DACQS2 application software.